はじめに
SEKIROみたいな剣の斬り合いがVRでやりたい!!!!
こんにちは、ZeniZeniです。
昨今、Sword Of GargantuaやSword Master VRなど、面白い良VR剣戟ゲームが増えてきました。
それらをプレイしてると、自分の理想の剣戟ゲームというのを作りたい欲がふつふつと湧き上がってきます。
というわけで絶賛開発中です。
今回は、VRで剣戟ゲームを作るための第一歩として、剣を高速で振っても、剣の当たり判定と剣同士が交差した座標を取得できる機能を実装しようと思います。
下の動画のようなことができるようになります。
この速度で当たり判定とるの苦労したができた!
— ZeniZeni (@ZeniYuki0922) November 13, 2019
めっっっっちゃ楽しい!!!
VR剣戟ゲーはこれくらい斬りあう感じが俺の理想
(音あり) pic.twitter.com/7ZMnJZBgdP
これは、剣が交差した瞬間の座標を取得して、その座標から火花のエフェクトを発生させています。
実装方法
実装方法ですが、コリダーは使わずにやっています。
なぜかというと、高速な物体同士の当たり判定は、コリダーだと簡単にすり抜けてしまうからです。
下の動画くらいの速度が限界でした。
SEKIROみたいに火花を散らすとめちゃめちゃ楽しいことに気づいた pic.twitter.com/B4hWueOCrl
— ZeniZeni (@ZeniYuki0922) November 12, 2019
プラス、座標を取得するために小さいコリダーを大量に配置していたので、剣を変えるときは設定がめんどくさいですし、パフォーマンスもよろしくなさそうです。
それではコリダーを使わない当たり判定の実装方法を考えていきましょう。
まず、剣と剣がぶつかった判定をどうとるかを考えてみます。
これは三次元空間において、ある線分と線分の距離が一定値以下になったときを考えればよさそうです。
剣同士の距離の導出
計算方法
それでは、$点(p_{11}, p_{12})$からなる線分$L_1$と、$点(p_{21}, p_{22})$からなる線分$L_2$の距離$d$を導出していきます。
こちらのサイトを参考にしてみます。
まず線分$L_1$の方向ベクトルを$V_1$、線分$L_2$の方向ベクトルを$V_2$として、$V_1$と$V_2$の外積、すなわち線分$L_1$から線分$L_2$に垂直なベクトル$n$を求めます。
$L_1$上の任意の点$P_1$から$L_2$上の任意の点$P_2$へのベクトルを$V_{12}$とすれば、ベクトル$n$とベクトル$V_{12}$の内積が、そのまま距離$d$となります。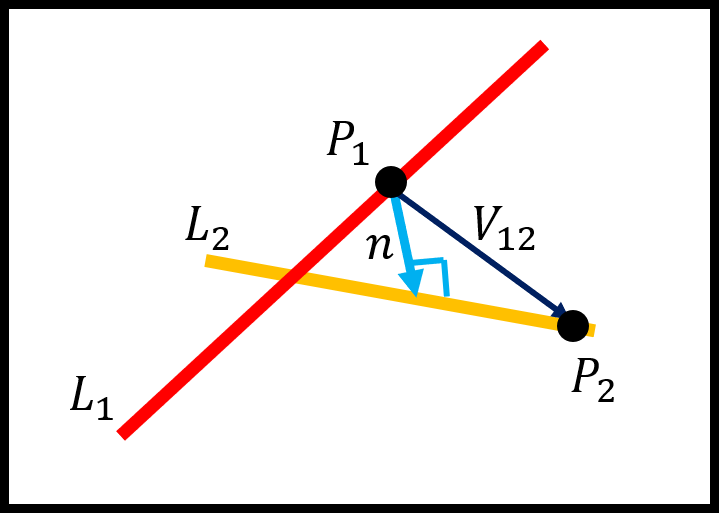
計算がうまくできないとき
上記の導出では、線分同士が同一平面上にあるときには距離$d$は必ず0になり、正確な値が出ません。
ベクトル$V_{12}$とベクトル$n$が垂直になり、内積$(V_{12},n) = 0$となるからです。(垂直なベクトルの内積は0)
実際の所、剣同士をぶんぶん振り回している中で、剣同士が同一平面上になるときなど滅多にないのですが、一応考慮しておきます。
剣同士が交差した座標の導出
計算方法
火花を剣同士がぶつかった瞬間にぶつかった場所から発生させたいので、剣同士が交差した座標を導出していきます。
これがちょっとめんどくさいです。
考え方としては、まず線分$L_2$上の点で、線分$L_1$に最も近い点を$P_{min}$とします。その点$P_{min}$上から線分$L_1$への垂線の方向ベクトルの単位ベクトルを$\hat{n}$とします。
剣同士の交点ですが、例えば剣同士が10cmより小さくなったときを剣同士が接触したと考えれば、剣同士の交点は剣同士の互いに最も近い点二つの中点とするのがよさそうです。
ゆえに交点$M$は、剣同士の距離を$d$とすれば
M = P_{min} + \frac{d}{2} * \hat{n}
となります。
それでは次に、$P_{min}$を導出していきます。
まず、線分$L1$上の任意の点$P_1$は、線分$L_1$の始点$P_{11}$の$x$座標を$P_{11x}$、線分$L_1$の方向ベクトル(始点$P_{11} - $ 終点$P_{12}$)の$x$成分を$v_{1x}$のようにあらわすとして、状態変数$t_1$$(0 \leqq t_1 \leqq 1)$を用いれば
\begin{align}
P_1 &= (l_{1x},l_{1y},l_{1z}) \\
&= (p_{11x} + t_1v_{1x},p_{11y} + t_1v_{1y},p_{11z} + t_1v_{1z}) \\
\end{align}
と表せます。
また線分$L2$上の任意の点$P_2$も同様にして
\begin{align}
P_2 &= (l_{2x},l_{2y},l_{2z}) \\
&= (p_{21x} + t_2v_{2x},p_{21y} + t_2v_{2y},p_{21z} + t_2v_{2z}) \\
\end{align}
と表せます。
すると距離$d$は
\begin{align}
d^2 &= (l_{1x} - l_{2x})^2 + (l_{1y} - l_{2y})^2 +(l_{1z} - l_{2z})^2 \\
&= (v_{1x}^2 + v_{1y}^2 + v_{1z}^2)t_1^2 \\
& \quad \quad + 2(v_{1x}v_{2x} + v_{1y}v_{2y} + v_{1z}v_{2z})t_1t_2 \\
& \quad \quad + 2(v_{1x}(p_{11x} - p_{21x}) + v_{1y}(p_{11y} - p_{21y}) + v_{1z}(p_{11z} - p_{21z}))t_1 \\
& \quad \quad + (v_{2x}^2 + v_{2y}^2 + v_{2z}^2)t_2^2 \\
& \quad \quad + 2(v_{2x}(p_{21x} - p_{11x}) + v_{2y}(p_{21y} - p_{11y}) + v_{2z}(p_{21z} - p_{11z}))t_2 \\
& \quad \quad + (p_{11x}-p_{21x})^2 + (p_{11y}-p_{21y})^2 + (p_{11z}-p_{21z})^2
\end{align}
というようにあらわせます。
うへぇ…って思いますよね、僕は思いました。
これを次数に注目して、係数は適当な文字に置き換えて、平方完成してみます。
\begin{align}
d^2 &= At_1^2 + Bt_1 + Ct_1t_2 + Dt_2^2 + Et_2 + F \\
&= A\biggr(t_1 + \frac{C}{2A}t_2 + \frac{B}{2A}\biggr)^2 + \biggr(D - \frac{C^2}{4A}\biggr)\biggr(t_2 + \frac{E - \frac{2BC}{4A}}{2D-\frac{C^2}{4A}}\biggr)^2 -\frac{B^2}{4A} + F
\end{align}
今求めようとしている点$P_{min}$は、$d$が最小のとき、すなわち平方完成した部分が0になるときなので、
\begin{align}
t_2 &= - \frac{E - \frac{2BC}{4A}}{2D-\frac{C^2}{4A}} \\
&= \frac{BC - 2AE}{4AD - C^2}
\end{align}
のときです。
したがって$P_{min}$は$P_2 = (p_{21x} + t_2v_{2x},p_{21y} + t_2v_{2y},p_{21z} + t_2v_{2z})$の$t_2$に$\frac{BC - 2AE}{4AD - C^2}$を代入したものとなります。
絶対に交差しないとき
剣が絶対に交差しない状況のときは上のような計算をするのは無駄なので、そのような状況は早い段階ではじきましょう。
剣が絶対に交差しない状況は、下図のようなときです。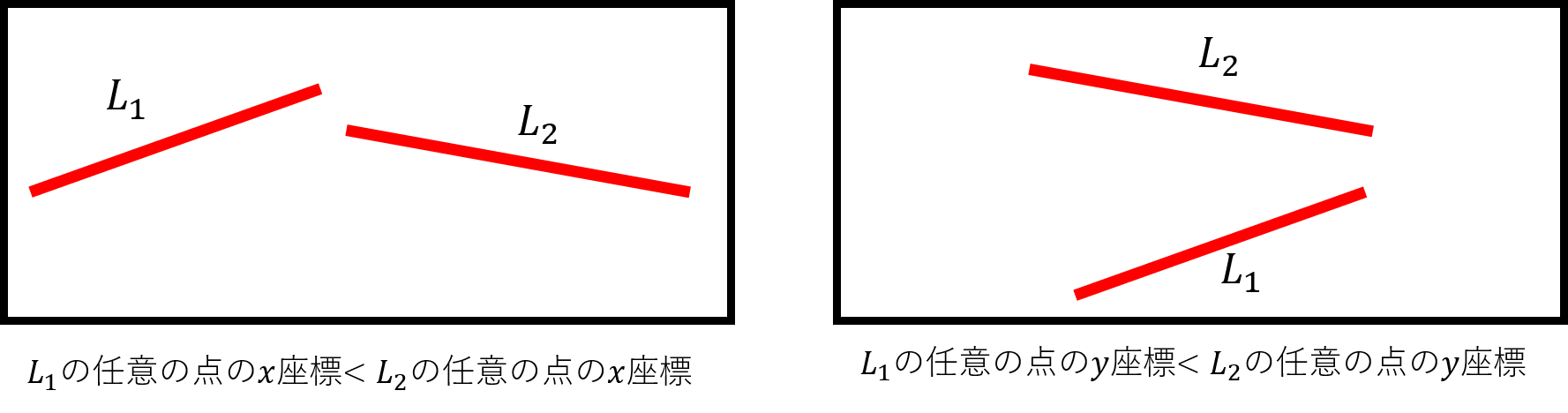
これにz座標の判定も加わります。
実際のコード
それでは実際に書いた線分同士の距離と交点を導出するコードがこちらです。
線分同士の距離とその交点を同時に取得したかったので、IntersectionInfoという構造体を作っています。
線分はLineという構造体を作成していて、剣の刃の部分の根本と剣先の2点を設定してください。
usingSystem.Collections;usingSystem.Collections.Generic;usingUnityEngine;usingSystem;[Serializable]publicstructLine{publicTransformp1;publicTransformp2;}publicstructIntersectionInfo{publicfloatDistance;publicVector3MidPoint;}publicclassIntersectionChecker:MonoBehaviour{publicLinel1;publicLinel2;publicIntersectionInfoinfo;// Start is called before the first frame updatevoidStart(){}// Update is called once per framevoidUpdate(){if(Input.GetKeyDown(KeyCode.Space)){vart=GetIntersectionInfo(l1,l2);Debug.Log("distance is "+t.Distance);Debug.Log("mid point is "+t.MidPoint);}}publicIntersectionInfoGetIntersectionInfo(Lineline1,Lineline2,floatdThreshold=0.5f){//各平面で交差していない時は排除if(!CheckIntersectionException(line1,line2)){Debug.Log("not intersect");info.Distance=-1;returninfo;}Debug.Log("intersect!");varp11=line1.p1.position;varp12=line1.p2.position;varp21=line2.p1.position;varp22=line2.p2.position;varv1=p12-p11;varv2=p22-p21;varv12=p22-p11;varn=Vector3.Cross(v1,v2).normalized;vard=Mathf.Abs(Vector3.Dot(n,v12));//線分同士が同一平面上にあるときif(d==0){if(IsInSamePlane(line1,line2)){Debug.Log("lines are in same plane");info.Distance=-1;returninfo;}}//dThresholdより離れている時を排除if(d>dThreshold){info.Distance=-1;returninfo;}info.Distance=d;//線分ががもう一つの線分に対して手前か奥にあるかの判定varside=(Vector3.Cross(v1,v12).y<0?1:-1);vartmpA=v1.x*v1.x+v1.y*v1.y+v1.z*v1.z;vartmpB=2*(v1.x*(p11.x-p21.x)+v1.y*(p11.y-p21.y)+v1.z*(p11.z-p21.z));vartmpC=2*(v1.x*v2.x+v1.y*v2.y+v1.z*v2.z);vartmpD=v2.x*v2.x+v2.y*v2.y+v2.z*v2.z;vartmpE=2*(v2.x*(p21.x-p11.x)+v2.y*(p21.y-p11.y)+v2.z*(p21.z-p11.z));//var t2 = -( tmpE - ( (2 * tmpB * tmpC) / (4 * tmpA) ) ) / ( 2 * (tmpD - ( (tmpC * tmpC ) / (4 * tmpA) )) );vart2=(tmpB*tmpC-2*tmpA*tmpE)/(4*tmpA*tmpD-tmpC*tmpC);Debug.Log("P min is "+(p21+(t2*v2)));info.MidPoint=p21+(t2*v2)+((d/2)*side*n);returninfo;}publicboolIsInSamePlane(Lineline1,Lineline2){varp1=line1.p1.position;varp2=line1.p2.position;varp3=line2.p1.position;varp4=line2.p2.position;varv1=p2-p1;varv2=p3-p1;varv3=p4-p1;vardet=(v1.y*v2.z*v3.x)+(v1.z*v2.x*v3.y)+(v1.x*v2.y*v3.z)-(v1.z*v2.y*v3.x)-(v1.x*v2.z*v3.y)-(v1.y*v2.x*v3.z);returndet==0;}publicboolCheckIntersectionException(Lineline1,Lineline2){varp1=line1.p1.position;varp2=line1.p2.position;varp3=line2.p1.position;varp4=line2.p2.position;//x座標チェックif(p1.x<=p2.x){if((p3.x<p1.x&&p4.x<p1.x)||(p2.x<p3.x&&p2.x<p4.x)){returnfalse;}}else{if((p3.x<p2.x&&p4.x<p2.x)||(p1.x<p3.x&&p1.x<p4.x)){returnfalse;}}//y座標チェックif(p1.y<=p2.y){if((p3.y<p1.y&&p4.y<p1.y)||(p2.y<p3.y&&p2.y<p4.y)){returnfalse;}}else{if((p3.y<p2.y&&p4.y<p2.y)||(p1.y<p3.y&&p1.y<p4.y)){returnfalse;}}//z座標チェックif(p1.z<=p2.z){if((p3.z<p1.z&&p4.z<p1.z)||(p2.z<p3.z&&p2.z<p4.z)){returnfalse;}}else{if((p3.z<p2.z&&p4.z<p2.z)||(p1.z<p3.z&&p1.z<p4.z)){returnfalse;}}returntrue;}}}という感じになります。
交差しない場合やいくつかの例外時には、IntersectionInfoのDistanceは-1となります。
下図のような感じで設定してください。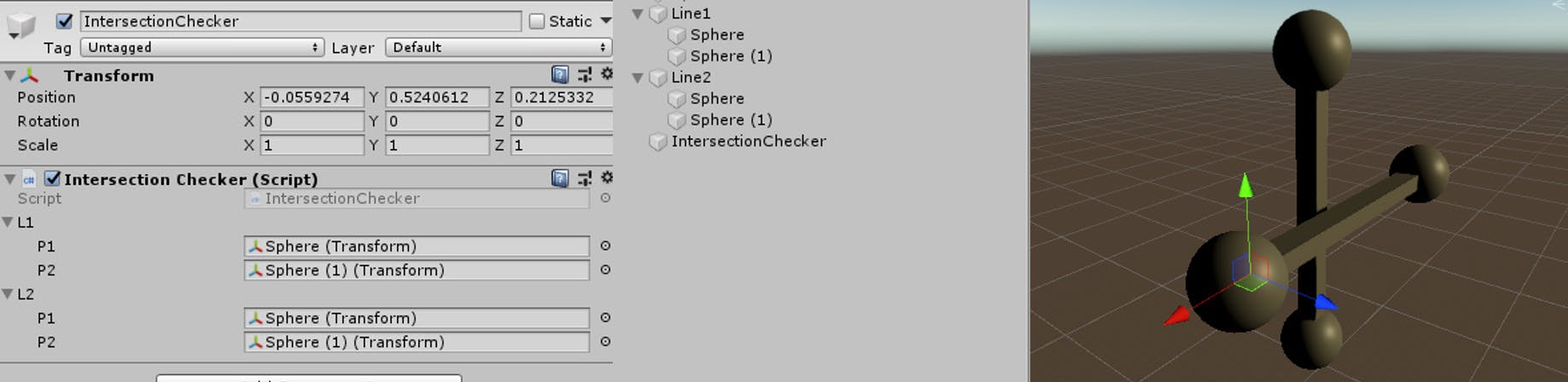
後は、GetIntersectionInfo関数を呼んで得られたIntersectionInfoのMidPointで火花等のエフェクトを発生させればよいのです。
剣を速く振ったときだけ呼びたい場合、まず剣の振る速度を求める方法を考えると思います。
剣の振る速度は、SteamVR SDKアセットに入っている、VelocityEstimatorというコンポーネントを使うことをお勧めします。